standardize documentation
standardize removes the mean of a variable and scales it such that its standard deviation is 1. This operation is sometimes known as "centering and scaling".
Back to Climate Data Tools Contents.
Contents
Syntax
Xs = standardize(X) Xs = standardize(...,dim) Xs = standardize(...,nanflag) Xs = standardize(...,'weighting',w) [Xs,mu] = standardize(...)
Description
Xs = standardize(X) subtracts the mean of X from X, then divides by the standard deviation of X.
Xs = standardize(...,dim) specifies a dimension along which to operate. Standardization is along the first nonsingleton dimension by default.
Xs = standardize(...,nanflag) specifies whether to include or omit NaN values from the calculation for any of the previous syntaxes. standardize(X,'includenan') includes all NaN values in the calculation while standardize(X,'omitnan') ignores them. Default behavior is 'includenan'.
Xs = standardize(...,'weighting',w) specifies a weighting scheme w for the calculation of the standard deviation. When w = 0 (default), S is normalized by N-1. When w = 1, S is normalized by the number of observations, N. w also can be a weight vector containing nonnegative elements. In this case, the length of w must equal the length of the dimension over which std is operating.
[Xs,mu] = standardize(...) returns mu mean and standard deviation of X. If X is a vector, mu(1) is the mean of X and mu(2) is the standard deviation of X. If X is multidimensional, the mean is the first entry in the direction of operation and std is the second entry. In other words, if X is three dimensional and is standardized alnog the third dimension, mu(:,:,1) is the mean and mu(:,:,2) is the standard deviation of X.
Example 1: 1D time series
Here's a time series:
x = 1:700; y = 15*sind(x)+3*randn(size(x))+300; plot(x,y)
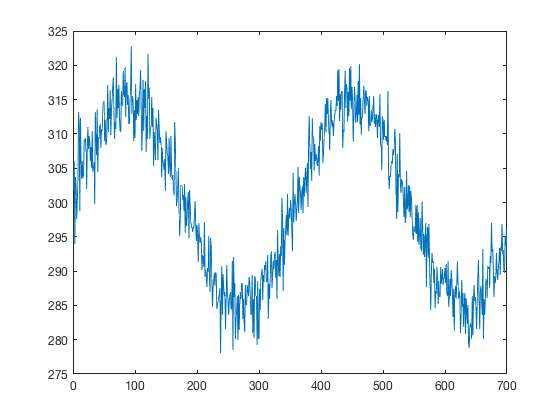
In the figure above, you can see that the mean of y is about 300 and the standard deviation is about 10. Standardize y like this:
ys = standardize(y); plot(x,ys)
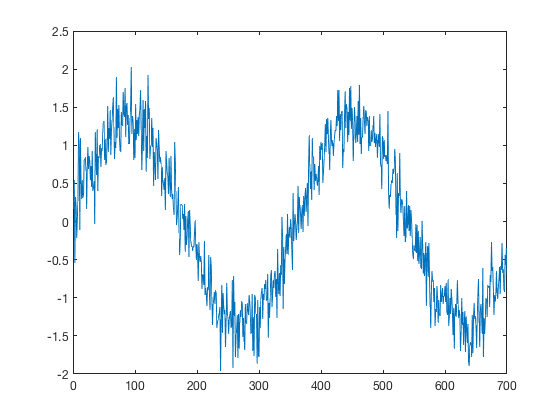
Now the signal oscillates around 0 and its standard deviation is 1.
Example 2: 1D time series with a trend
What if your time series has a trend in it? Like this:
x = 1:1080; y = 15*sind(x)+3*randn(size(x))+300 +x/5; plot(x,y)
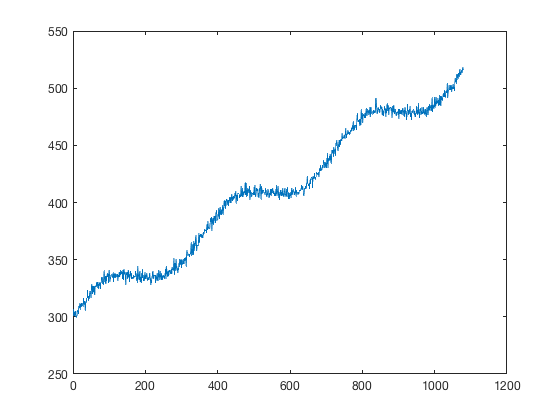
It's important to note that standardizing and then detrending does not produce the same result as detrending and then standardizing. Here's the difference:
% standardize y: ys = standardize(y); % detrend the standardized y: ysd = detrend(ys); plot(x,ysd) legend('standardized then detrended')
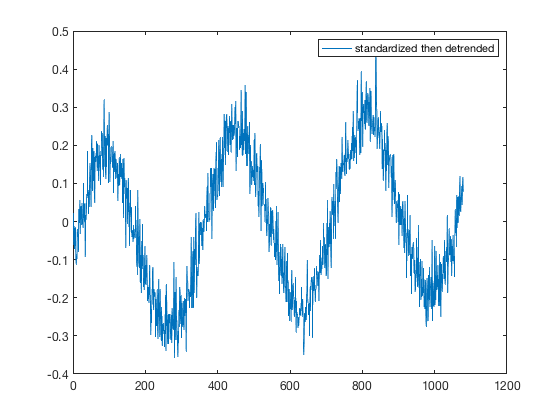
yd = detrend(y); yds = standardize(yd); hold on plot(x,yds) legend('standardized then detrended',... 'detrended then standardized')

The end results, ysd and yds both have mean values of 0, but the standard deviation of ysd is smaller than 1 because it was detrended after standardization.
Example 3:
Consider this sample sea surface temperature dataset that is 60x55x802 in size. Begin by plotting the mean and standard deviation of the raw sst dataset:
load pacific_sst figure subplot(1,2,1) imagescn(lon,lat,mean(sst,3)) cmocean thermal cb(1) = colorbar('location','northoutside'); xlabel(cb(1),'mean sst (\circC)') subplot(1,2,2) imagescn(lon,lat,std(sst,[],3)) cmocean amp cb(2) = colorbar('location','northoutside'); xlabel(cb(2),'\sigma sst (\circC)')
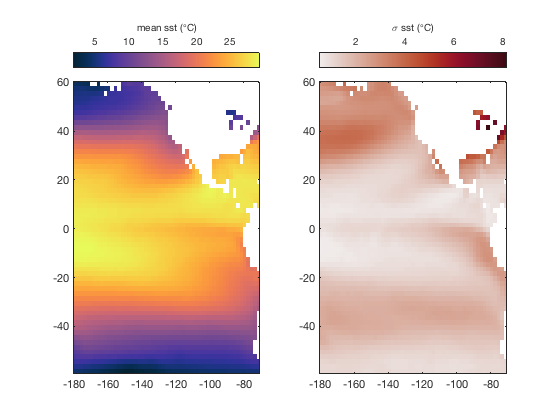
The maps above show about what we'd expect: On average it's warm close to the equator and cooler toward the poles. The North American Great Lakes, which are quite chilly on average, have the greatest sst variability because they freeze in winter but warm up nicely in the summer.
If you want to center and scale this SST dataset,
% Standardize sst along dimension 3: sst_s = standardize(sst,3); figure subplot(1,2,1) imagescn(lon,lat,mean(sst_s,3)) cmocean thermal cb(1) = colorbar('location','northoutside'); xlabel(cb(1),'mean sst (\circC)') subplot(1,2,2) imagescn(lon,lat,std(sst_s,[],3)) cmocean amp cb(2) = colorbar('location','northoutside'); xlabel(cb(2),'\sigma sst (\circC)')

The plot above on the left shows that the mean of the sst after it has been centered and scaled is just numerical noise. That's a characteristic noise pattern that should always encourage you to check the scientific notation on the colorbar axes.
And on the right, the standard deviation is 1 everywhere. That's because that's exactly what we set it to be with standardize.
Author Info
This function is part of the Climate Data Toolbox for Matlab. The function and supporting documentation were written by Chad A. Greene of the University of Texas at Austin.